(ア)
Yiは、マス目Xiまで経路がえられているときの、移動できるマス目の集合である。
処理Bが「元に戻る」処理であると考えられるので、そうだと分かる。
よってR(S)。
処理Aは、Sから始め、Gに達するまで経路を探し続ける処理である。
だからXiがGと等しくない間処理を続ける。
変数Yiが空集合の場合、「元に戻る」。
処理Bは、iをi-1にして「元に戻る」。
戻ってから処理を続けるとき、すでに行き止まりになっている経路を再び選ばないために、YiをYi-{P}にしておく必要がある。
Xi+1をPにしてみる。
Yi+1をR(P)-{Xi}にする。逆戻りしないようにするためである。
そして、iをi+1にして次なる探索を行う。
(イ)
下図のような迷路を例にとり考える。
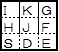
・処理Cの実行回数が最小になる推移
Sから始めると
X1=S
Y1={D,H}
i=1
X1≠Gであるから処理Aを実行する。
Y1が空集合でないから処理Cを実行する(1回目)。
Y1からDを選ぶと
Y1={D,H}-{D}={H}
X2=D
Y2={E,J,S}-{S}={E,J}
i=2
X2≠Gであるから処理Aを実行する。
Y2が空集合でないから処理Cを実行する(2回目)。
Y2からEを選ぶと
Y2={E,J}-{E}={J}
X3=E
Y3={D,F}-{D}={F}
i=3
X3≠Gであるから処理Aを実行する。
Y3が空集合でないから処理Cを実行する(3回目)。
Y3からFを選ぶと
Y3={F}-{F}=空集合
X4=F
Y4={E,G}-{E}={G}
i=4
X4≠Gであるから処理Aを実行する。
Y4が空集合でないから処理Cを実行する(4回目)。
Y4からGを選ぶと
Y4={G}-{G}=空集合
X5=G
Y5={F}-{F}=空集合
i=5
X5=Gだから終了。
よって処理Cの実行回数の最小値は4。
同様に考えると、大きさnのときは
(n-1)×2 = 2n-2
・処理Bの実行回数が最大になる推移
Sから始めると
X1=S
Y1={D,H}
i=1
X1≠Gであるから処理Aを実行する。
Y1が空集合でないから処理Cを実行する。
Y1からHを選ぶと
Y1={D,H}-{H}={D}
X2=H
Y2={I,S}-{S}={I}
i=2
X2≠Gであるから処理Aを実行する。
Y2が空集合でないから処理Cを実行する。
Y2からIを選ぶと
Y2={I}-{I}=空集合
X3=I
Y3={H}-{H}=空集合
i=3
X3≠Gであるから処理Aを実行する。
Y3が空集合だから処理Bを実行して(1回目)
i=2
Y2が空集合だから処理Bを実行して(2回目)
i=1
X1≠Gであるから処理Aを実行する。
Y1が空集合でないから処理Cを実行する。
Y1からDを選ぶと
Y1={D}-{D}=空集合
X2=D
Y2={E,J,S}-{S}={E,J}
i=2
X2≠Gであるから処理Aを実行する。
Y2が空集合でないから処理Cを実行する。
Y2からJを選ぶと
Y2={E,J}-{J}={E}
X3=J
Y3={D,K}-{D}={K}
i=3
X3≠Gであるから処理Aを実行する。
Y3が空集合でないから処理Cを実行する。
Y3からKを選ぶと
Y2={K}-{K}=空集合
X4=K
Y4={J}-{J}=空集合
i=4
X4≠Gであるから処理Aを実行する。
Y4が空集合だから処理Bを実行して(3回目)
i=3
Y3が空集合だから処理Bを実行して(4回目)
i=2
X2≠Gであるから処理Aを実行する。
Y2が空集合でないから処理Cを実行する。
Y2からEを選ぶと
Y2={E}-{E}=空集合
X3=E
Y3={D,F}-{D}={F}
i=3
Eを選んだあとは、最初の推移と同じで、処理Bは実行されない。
以上のように、最短経路以外はすべて行き止まりになるとき、処理Bの実行回数が最大になることが分かる。
よって処理Bの実行回数の最大値は4。
同様に考えると、大きさnのときは






コメントを残す